Introducción¶
Si tienes experiencia en el uso de frameworks de redes neuronales como PyTorch, TensorFlow o Keras sabrás que existe una feature muy importante e interesante llamada AutoGrad, la cual, además de optimizar el calculo de gradientes en tiempo de ejecución, permite modularizar los gradientes para facilitar su retropropagción (o Backpropagation en inglés). Así, si ya están definidos los gradientes de las funciones de activación y funciones de costo, es fácil aplicar la regla de cadena para ajustar los parámetros desde la última capa hacia la primera.
En esta entrega en realidad no se revisa como funciona AutoGrad, si no, se hace un desarrollo matemático de los gradientes resultantes que se utilizan para actualizar una red neuronal pequeña como si estuviéramos resolviendo un problema específico en un contexto en el que no existen librerías como estas. Sin embargo, si estás más interesado en saber cómo programar tu propio AutoGrad, te recomiendo esta serie de videos.
Red Neuronal poco profunda para la clasificación de dígitos escritos a mano.¶
Digamos que queremos clasificar muestras del conjunto de datos escritos a mano MNIST de Yann LeCun (un científico muy importante en el desarrollo de redes neuronales artificiales y actual jefe de Meta AI). Este conjunto de datos consiste de muchas imágenes a escalas de grises de los 10 dígitos (0, 1, ..., 9). Cada imágen tiene 784 pixeles, entonces la red neuronal tendrá 784 neuronas en su capa de entrada y 10 neuronas en su capa de salida (una por cada dígito).
Históricamente, las redes neuronales artificiales iniciaron con el modelo de neurona de McCulloch y Pitts:
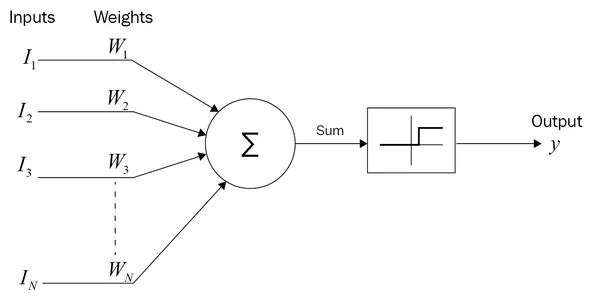
McCulloch y Pitts partieron de la idea de que la mente se podría explicar con lógica y había indicios de que las conexiones entre las neuronas tienen pesos (sinápticos) que ponderan las señales y realizan procesos químicos para modificar el resultados de esta ponderación (como lo hace la función de activación). Aunque McCulloch y Pitts estaban equivocados en sus ideas del cerebro, su modelo de neurona funcionó para establecer las bases de la estructura básica de las capas de las neuronas. De manera general usamos la siguiente expresión matemática:
$$ y = f(b_0 + b_1 x_1 + b_2 x_2 + \dots b_n x_n) $$
Donde $f$ es una función de activación, $x$ son las entradas de la red y los coeficientes $b$ son pesos que ponderan la importancia de cada entrada. Algunas funciones de activación que se utilizan en la actualidad son sigmoide, tanh (tangente hiperbólica) y ReLu (con sus muchas variantes). Siendo ReLu la más popular en la actualidad. Aquí usamos sigmoide por cuestiones matemáticas, pues calcular su derivada es muy fácil.
$$ \text{sigmoide(x)} = \phi(x) = \frac{1}{1 + e^{-x}} $$
Usando aritmética de matrices, se puede reescribir la ecuación de arriba con un producto matricial en lugar de una suma ponderada:
$$ \mathbf y = f(b_0 + b_1 x_1 + b_2 x_2 + \dots b_n x_n) = f(\mathbf xw + b) $$
En un problema de clasificación de varias clases no se tiene una sola salida $y$, sino varias, así que en lugar de tener un valor numérico como respuesta del modelo, se tiene una serie de valores agrupados como un vector $\mathbf y$ y se necesita una matriz de pesos $W$ para conectar cada neruona de entrada con todas las neuronas de salida de la misma capa. Y cuando se tiene que cada dato del conjunto de datos contiene muchísimas variables (cada pixel es una variable diferente) con una estructura muy complicada de diferenciar (como lo son las formas de los dígitos) es necesario agregar más capas para que la red neruonal sea más capaz de reconocer estructuras complejas. En general, tendremos una serie de capas apiladas que matemáticamente se ve como sigue:
\begin{align*} \mathbf y_1 &= f_1(\mathbf xW_1 + b_1) \\ \mathbf y_2 &= f_2(\mathbf y_1W_2 + b_2) \\ \vdots \\ \hat y = y_n &= f_n(\mathbf y_{n-1}W_n + b_n) \end{align*}
A esta apilación de funciones se le conoce como Perceptrón Multicapa (Multi-layer Perceptron). Y se visualiza de la siguiente forma:
Uno de los problemas más grandes en la teoría de las redes neuronales es el proceso de ajuste o algoritmo de entrenamiento de los parámetros $W$ y $b$ de la red. El algoritmo más común se basa en el descenso de gradiente. Matemáticamente, el gradiente de una función representa la dirección en la cual incrementa más el valor de una función, y la dirección contraria a esta es la dirección en donde más desciende. Entonces al calcular el gradiente, sabemos hacia que dirección se deben modificar los parámetros del modelo para reducir el error de predicción. No obstante, esto implica que se requiere de una función que mida el error de predicción. Probablemente estés familiarizado con el valor cuadrático medio (RMS en inglés), la entropía cruzada binaria (binary cross-entropy) y la entropía cruzada categórica (categorical cross-entropy).
Además de que queremos que se minimice el error cuando el modelo es mejor, existe un fundamento matemático para proponer funciones de error (costo o pérdida, estos nombres derivan de la noción de perder dinero cuando tomamos una mala decisión), y este fundamento es la estimación de máxima verosimilitud (o Maximum Likelihood Estimation). Es decir, en lugar de sólo reducir el error de predicción, queremos aumentar la probabilidad de que nuestro modelo se parezca al modelo verdadero en base a los datos y resultados que nos arroja. Matemáticamente maximar la verosimilitud resulta en las mismas ecuaciones de minimizar las funciones de costos de RMS, Entropía cruzada binaria y Entropía cruzada binaria categórica.
En este caso, la función de costo que aumenta la verosimilitud de un modelo de clasificación de varias clases es la Entropía cruzada binaria categórica:
$$ L = - \sum_i^{10} t_i log(\hat y_i) $$
10 es la cantidad de clases diferentes, i.e., dígitos; $t$ es el valor verdadero o label utilizando codificación one-hot encoding, por ejemplo, $t=3$ y $t=7$ en esta codificación son:
\begin{align*} t = 3 &= [0, 0, 0, 1, 0, 0, 0, 0, 0, 0]\\ t = 7 &= [0, 0, 0, 0, 0, 0, 0, 1, 0, 0] \end{align*}
Por último, se minimiza el error tomando todas los datos y todos los resultados arrojados por el modelo. Pero existe una limitante, la cantidad de datos es demasiado grande, consume demasiada memoria RAM y requiere de multiplicaciones matriciales muy lentas. Por lo cual, es mejor tomar un subconjunto de datos para calcular el error y actualizar los pesos. A este proceso se le conoce como descenso de gradiente estocástico por lotes (Mini batch -stochastic- gradient descent).
Usar lotes involucra un cambio en la notación. Pues si un dato antes era un vector, ahora un conjunto de datos es una matriz representada con letras mayúsculas donde cada renglón es un dato diferente y cada columna corresponde a un píxel. Entonces, trabajando con lotes:
\begin{align*} Y_0 &= X\\ Z_1 &= Y_0W_1 + b_1\\ Y_1 &= \phi(Z_1)\\ Z_2 &= Y_1W_2 + b_2\\ Y_2 &= \text{softmax}(Z_2)\\ \hat Y &= Y_2 \end{align*}
Y la función de costo por batch de $m$ muestras:
$$ L = -\sum_k^m \sum_i^{10} t_i^k log(\hat y_i^k) $$
Y el superíndice $k$ usado en $t_i^k$ y $\hat t_i^k$ indican que corresponde al resultado usando la muestra $k$.
Descenso de gradiente¶
El algoritmo de descenso de gradiente es bastante sencillo. Una vez que se tiene una dirección de descenso (como la dirección contraria al gradiente), modificar los parámetros en esa dirección, usando un cambio suficientemente pequeño se asegura que la función de costo siempre se va a reducir en cada actualización. Es decir, si $\alpha$ es suficientemente pequeño, la siguiente ecuación asegura que se reducirá la función de costo:
$$ \theta_{k+1} = \theta_{k+1} - \alpha \nabla_\theta L $$
Donde $\theta$ es cualquier parámetro $W_1$, $b_1$, $W_2$, $b_2$ y $\nabla_\theta L$ es el gradiente de la función de costo con respecto a ese parámetro.
Este es el algoritmo sencillo de descenso de gradiente. Puedes utilizarlo y funcionará en este problema. Sin embargo, existen algoritmos mejorados con mejores cualidades y que encuentran soluciones más rápidamente. Debido al propósito que tienen estas funciones, se les conocen como optimizadores (en pytorch los encuentras en el submódilo optim). Un optimizador que ha ganado mucha popularidad es ADAMW:

Este optimizador se realiza para cada parámetro, entonces los parámetros $b_1, W_1, b_2, W_2$ tendrán sus propias variables $m$ (momentos) y $v$ (velocidades) para actualizar. Se utilizarán los mismos híperparámetros para todos los conjuntos de momentos.
Si quieres ver qué tan rápido es el optimizador ADAMW comparado con otros, ve este vídeo de una animación que hice. Puedes ver cómo unos optimizadores descienden más rápido que otros
Cálculo de los gradientes¶
Calculando los gradientes para actualizar los parámetros:
\begin{align*} \frac{\partial L}{\partial W_{2_{a,b}}} &= \sum_k^m \frac{\partial L^k}{\partial W_{2_{a,b}}} = - \sum_k^m \frac{\partial L^k}{\partial Z^k_{2_b}} \cdot \frac{\partial Z^k_{2_b}}{\partial W_{2_{a,b}}} \\ &= \sum_k^m (\hat y^k_b - t^k_b) Y^k_{1_a} \\ \nabla_{W_2} L &= \begin{bmatrix} \sum_k^m (\hat y^k_1 - t^k_1) Y^k_{1_1} & \dots & \sum_k^m (\hat y^k_{10}- t^k_{10}) Y^k_{1_1} \\ \vdots & \ddots & \vdots \\ \sum_k^m (\hat y^k_1 - t^k_1) Y^k_{1_p} & \dots & \sum_k^m (\hat y^k_{10}- t^k_{10}) Y^k_{1_p} \end{bmatrix} \\ &= \begin{bmatrix} Y^1_{1_1} & \dots & Y^m_{1_{1}} \\ \vdots & \ddots & \vdots \\ Y^1_{1_{p}} & \dots & Y^m_{1_{p}} \\ \end{bmatrix} \begin{bmatrix} \hat y^1_1 - t^1_1 & \dots & \hat y^1_{10} - t^1_{10} \\ \vdots & \ddots & \vdots \\ \hat y^m_{1} - t^m_{1} & \dots & \hat y^m_{10} - t^m_{10} \end{bmatrix} \\ &= Y_1^T(\hat Y - T) \\ \frac{\partial L}{\partial b_{2_{j}}} &= - \sum_k^m \frac{\partial L^k}{\partial Z^k_{2_j}} \cdot \frac{\partial Z^k_{2_j}}{\partial b_{2_{j}}} \\ &= - \sum_k^m (\hat y^k_b - t^k_b) \cdot 1\\ \nabla_{b_2} L &= \mathbf 1^T(\hat Y - T) \end{align*}
Con respecto a los parámetros $W_1$ y $b_1$, los cálculos son más complicados.
\begin{align*} \frac{\partial L}{\partial W_{1_{a, b}}} &= \sum_k^m \frac{\partial L^k}{\partial Z^k_{1_b}} \cdot \frac{\partial Z^k_{1_b}}{\partial W_{1_{a, b}}} \\ &= \sum_k^m \left(\sum_l^{10} \frac{\partial L^k}{\partial Z^k_{2_l}} \cdot \frac{\partial Z^k_{2_l}}{\partial Y^k_{1_b}} \cdot \frac{\partial Y^k_{1_b}}{\partial Z^k_{1_b}} \right) \cdot \frac{\partial Z^k_{1_b}}{\partial W_{1_{a, b}}} \\ &= \sum_k^m \left(\sum_l^{10} (\hat y^k_{l} - t^k_l)W_{2_{b, l}} Y^k_{1_b}(1 - Y^k_{1_b}) \right) Y^k_{0_a} \\ &= \sum_k^m Y^k_{1_b}(1 - Y^k_{1_b}) \left(\sum_l^{10} (\hat y^k_{l} - t^k_l)W_{2_{b, l}} \right)Y^k_{0_a} \\ &= \sum_k^m Y^k_{1_b}(1 - Y^k_{1_b})(\hat y^k - t^k)(W_{2_{b,:}})^T Y^k_{0_a} \\ &= \left(\sum_k^m Y^k_{0_a} Y^k_{1_b}(1 - Y^k_{1_b})(\hat y^k - t^k) \right) (W_{2_{b,:}})^T \\ \end{align*}
\begin{align*} \nabla_{W_1} L &= \begin{bmatrix} \left(\sum_k^m Y^k_{0_1} Y^k_{1_1}(1 - Y^k_{1_1})(\hat y^k - t^k) \right) (W_{2_{1,:}})^T & \dots & \left(\sum_k^m Y^k_{0_1} Y^k_{1_p}(1 - Y^k_{1_p})(\hat y^k - t^k) \right) (W_{2_{p,:}})^T \\ \vdots & \ddots & \vdots \\ \left(\sum_k^m Y^k_{0_{784}} Y^k_{1_1}(1 - Y^k_{1_1})(\hat y^k - t^k) \right) (W_{2_{1,:}})^T & \dots & \left(\sum_k^m Y^k_{0_{784}} Y^k_{1_p}(1 - Y^k_{1_p})(\hat y^k - t^k) \right) (W_{2_{p,:}})^T \\ \end{bmatrix} \\ &= \sum_k^m \begin{bmatrix} \left(Y^k_{0_1} Y^k_{1_1}(1 - Y^k_{1_1})(\hat y^k - t^k) \right) (W_{2_{1,:}})^T & \dots & \left(Y^k_{0_1} Y^k_{1_p}(1 - Y^k_{1_p})(\hat y^k - t^k) \right) (W_{2_{p,:}})^T \\ \vdots & \ddots & \vdots \\ \left(Y^k_{0_{784}} Y^k_{1_1}(1 - Y^k_{1_1})(\hat y^k - t^k) \right) (W_{2_{1,:}})^T & \dots & \left(Y^k_{0_{784}} Y^k_{1_p}(1 - Y^k_{1_p})(\hat y^k - t^k) \right) (W_{2_{p,:}})^T \\ \end{bmatrix} \\ &= \sum_k^m (Y_0^k)^T\begin{bmatrix} \left(Y^k_{1_1}(1 - Y^k_{1_1})(\hat y^k - t^k) \right) (W_{2_{1,:}})^T & \dots & \left(Y^k_{1_p}(1 - Y^k_{1_p})(\hat y^k - t^k) \right) (W_{2_{p,:}})^T \end{bmatrix} \\ &= \sum_k^m (Y_0^k)^T \left( Y^k_1 \odot (1 - Y^k_1) \odot \begin{bmatrix} (\hat y^k - t^k)(W_{2_{1,:}})^T & \dots & (\hat y^k - t^k)(W_{2_{p,:}})^T \end{bmatrix} \right) \\ &= \sum_k^m (Y_0^k)^T \left(Y^k_1 \odot (1 - Y^k_1) \odot ((\hat y^k - t^k)(W_{2})^T )\right) \\ &= (Y_0^T) \left(Y_1 \odot (1 - Y_1) \odot ((\hat y - t)(W_{2})^T )\right) \\ \nabla_{b_1} L &= \mathbf 1^T \left(Y_1 \odot (1 - Y_1) \odot ((\hat y - t)(W_{2})^T )\right) \end{align*}
Probablemente no estés familiarizado con el símbolo $\odot$. En este contexto, representa una multiplicación elemento a elemento. Por ejemplo, cuando multiplicas dos matrices de numpy del mismo tamaño con el símbolo '*' obtienes una multiplicación elemento a elemento. Algunos matemáticos le llaman multiplicación de Hadamard.
En conclusión, se usarán los siguientes gradientes para actualizar los parámetros de la red:
\begin{align*} \nabla_{W_2} L &= Y_1^T(\hat Y - T)\\ \nabla_{b_2} L &= \mathbf 1^T (\hat Y - T) \\ \nabla_{W_1} L &= (Y_0^T) (Y_1 \odot (1 - Y_1) \odot ((\hat y - t)(W_{2})^T ))\\ \nabla_{b_1} L &= \mathbf 1^T (Y_1 \odot (1 - Y_1) \odot ((\hat y - t)(W_{2})^T )) \end{align*}
Notamos que son las mismas que en el problema de clasificación binaria con entropía cruzada binaria como función de costo y sigmoide como función de activación en la última capa.
Implementación en código¶
Cargar la base de datos MNIST¶
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
mnist = fetch_openml("mnist_784")
X, y = mnist.data, mnist.target.astype(int)
# Separar en conjuntos de entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
X_train = X_train.values
X_test = X_test.values
# Normalizar datos
X_train = X_train / 255.0
X_test = X_test / 255.0
# dimensiones de los conjuntos
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
(56000, 784) (56000,) (14000, 784) (14000,)
Codificación One-hot¶
def one_hot(a):
b = np.zeros((a.size, a.max() + 1))
b[np.arange(a.size), a] = 1
return b
y_train = one_hot(y_train)
Funciones de activación¶
def phi(x):
return 1 / (1 + np.exp(-x))
def softmax(x):
return np.exp(x)/np.sum(np.exp(x), axis=1).reshape(-1, 1)
Inicializar pesos y biases¶
input_size = X_train.shape[1]
hidden_size = 64
output_size = 10
W_1 = np.random.randn(input_size, hidden_size,)
b_1 = np.zeros((1, hidden_size))
W_2 = np.random.randn(hidden_size,output_size,)
b_2 = np.zeros((1,output_size))
Parámetros de entrenamiento¶
learning_rate = 1e-4
epochs = 100
batch_size = 32
adamw = True #habilita la actualización de parámetros con ADAMW
weight_decay = 0.01
beta_1 = 0.9
beta_2 = 0.999
e = 1e-9
Ciclo de entrenamiento¶
El siguiente código funcoiona para crear lotes de manera aleatoria que serán utilizados en una época de entrenamiento.
def batchify(x, y, batch_size):
samples = x.shape[0]
rand_idcs = np.random.shuffle(list(range(samples)))
rand_x = x[rand_idcs]
rand_y = y[rand_idcs]
split_idcs = list(range(batch_size, samples, batch_size))
return zip(
np.split(x, split_idcs),
np.split(y, split_idcs)
)
#------------------------
#Inicialización de ADAMW.
mb1 = np.zeros_like(b_1)
vb1 = np.zeros_like(b_1)
mW1 = np.zeros_like(W_1)
vW1 = np.zeros_like(W_1)
mb2 = np.zeros_like(b_2)
vb2 = np.zeros_like(b_2)
mW2 = np.zeros_like(W_2)
vW2 = np.zeros_like(W_2)
#Fin de inicialización de ADAMW
#------------------------
Losses=[]
for epoch in range(1, epochs + 1):
loss = 0
for y_0, y in batchify(X_train, y_train, 32):
# Propagación hacia adelante, Eqs. (1)
z_1 = y_0 @ W_1 + b_1
y_1 = phi(z_1)
z_2 = y_1 @ W_2 + b_2
y_2 = softmax(z_2)
# Evaluar la pérdida
loss += -np.sum(y * np.log(y_2))/len(X_train)
# Backpropagation
delta_2 = y_2-y
delta_1 = np.dot(delta_2, W_2.T) * (y_1*(1-y_1))
grad_W2 = np.dot(y_1.T, delta_2)
grad_b2 = np.sum(delta_2, axis=0)[0]
grad_W1 = np.dot(y_0.T, delta_1)
grad_b1 = np.sum(delta_1, axis=0)[0]
#--------------------------
# Actualización de momentos de ADAMW.
beta_1_t = beta_1**epoch
beta_2_t = beta_2**epoch
mW2 = beta_1*mW2 + (1 - beta_1)*grad_W2
vW2 = beta_2*vW2 + (1 - beta_2)*grad_W2**2
hat_mW2 = mW2/(1 - beta_1_t)
hat_vW2 = vW2/(1 - beta_2_t)
mb2 = beta_1*mb2 + (1 - beta_1)*grad_b2
vb2 = beta_2*vb2 + (1 - beta_2)*grad_b2**2
hat_mb2 = mb2/(1 - beta_1_t**epoch)
hat_vb2 = vb2/(1 - beta_2_t**epoch)
mW1 = beta_1*mW1 + (1 - beta_1)*grad_W1
vW1 = beta_2*vW1 + (1 - beta_2)*grad_W1**2
hat_mW1 = mW1/(1 - beta_1_t)
hat_vW1 = vW1/(1 - beta_2_t)
mb1 = beta_1*mb1 + (1 - beta_1)*grad_b1
vb1 = beta_2*vb1 + (1 - beta_2)*grad_b1**2
hat_mb1 = mb1/(1 - beta_1_t)
hat_vb1 = vb1/(1 - beta_2_t)
#--------------------------
# Paso de descenso de gradiente
if adamw:
#----------------------------
#Ajuste de parámetros con ADAMW. Código añadido
W_2 -= learning_rate*weight_decay*W_2
W_2 -= learning_rate*hat_mW2/(hat_vW2**0.5 + e)
b_2 -= learning_rate*weight_decay*b_2
b_2 -= learning_rate*hat_mb2/(hat_vb2**0.5 + e)
W_1 -= learning_rate*weight_decay*W_1
W_1 -= learning_rate*hat_mW1/(hat_vW1**0.5 + e)
b_1 -= learning_rate*weight_decay*b_1
b_1 -= learning_rate*hat_mb1/(hat_vb1**0.5 + e)
#Fin de ajuste de parámetros con ADAMW
#-----------------------------
else:
W_2 -= learning_rate * grad_W2
b_2 -= learning_rate * grad_b2
W_1 -= learning_rate * grad_W1
b_1 -= learning_rate * grad_b1
# Reporta avence cada 10 épocas
if epoch % 10 == 0:
print(f"Epoch {epoch}, Loss: {loss}")
Losses.append([epoch,loss])
Losses = np.array(Losses)
Epoch 10, Loss: 1.2785014435881914 Epoch 20, Loss: 0.8429631069268259 Epoch 30, Loss: 0.6443507566618546 Epoch 40, Loss: 0.5257638618139021 Epoch 50, Loss: 0.4462716784121067 Epoch 60, Loss: 0.38888704286060727 Epoch 70, Loss: 0.3450194603053407 Epoch 80, Loss: 0.31020563474546536 Epoch 90, Loss: 0.2816816286106931 Epoch 100, Loss: 0.25778044648477133
import matplotlib.pyplot as plt
plt.figure(figsize=(10,3))
plt.loglog(Losses[:,0],Losses[:,1])
plt.title('Evolución de la pérdida durante entrenamiento')
plt.grid(True, which="both")
plt.ylabel("Pérdida o Costo")
plt.xlabel("Época")
plt.show()
Prueba¶
z_1 = X_test @ W_1 + b_1
y_1 = phi(z_1)
z_2 = y_1 @ W_2 + b_2
y_2 = softmax(z_2)
# Convierte predicciones a probabilidades
predictions = np.argmax(y_2, axis=1)
y_test = np.array(y_test)
# Calcula Exactitud: porcentaje de clasificaciones correctas
accuracy = np.mean(predictions == y_test)
print(f"Exactitud de Prueba (Test accuracy): {accuracy * 100}%")
Exactitud de Prueba (Test accuracy): 91.43571428571428%
Conclusiones y trabajo futuro¶
Una arquitectura muy sencilla como un perceptrón multicapa poca profunda consigue excelentes resultados para clasificar imágenes de dígitos escritos a mano. Ciertamente, muchos de los dígitos son complicados de clasificar debido a la ambigüedad de la escritura, entonces no esperamos que el modelo sea completamente capaz de clasificar todos los dígitos de manera correcta. Como trabajo futuro, sería interesante reducir el tiempo de ejecución de entrenamiento.